TENSORIEL (CALCUL)

TENSORIEL (CALCUL)

Introduit en 1900 par G. Ricci-Curbastro et T. Levi-Civita, le calcul tensoriel est un puissant outil de l’analyse mathématique; très utile en mécanique classique, il est indispensable en mécanique relativiste.

Dans le présent article, E est une variété différentiable de dimension n . Rappelons rapidement ce que cela signifie, tout en renvoyant le lecteur à l’article VARIÉTÉS DIFFÉRENTIABLES pour une définition plus détaillée. Au voisinage de chaque point m ⁰ de E, on peut trouver un système de coordonnées locales, c’est-à-dire repérer chaque point m par ses n coordonnées u ¹(m ), ..., u ⁿ (m ). Mais, au voisinage de m ⁰, il existe une infinité de systèmes de coordonnées raisonnables; aucun d’eux ne joue, a priori, un rôle particulier. Notons v ¹(m ), ..., v ⁿ (m ) les coordonnées de m pour un autre système; il existe n fonctions indéfiniment dérivables 祥¹, ..., 祥ⁿ , définies sur un ouvert de Eⁿ , telles que, pour tout point m voisin de m ⁰ et pour tout j , 1 諒 j 諒 n , on ait:

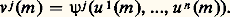Pour étudier la variété E, on choisit un système de coordonnées dans lequel on va faire les calculs; dans les formules que l’on écrira, on distinguera d’une part ce qui dépend du système de coordonnées choisi, et qui est en général dépourvu d’intérêt, d’autre part ce qui décrit des phénomènes intrinsèques. Parmi les plus importants des objets que l’on peut associer à une variété se trouvent les tenseurs qui sont définis dans l’article VARIÉTÉS DIFFÉRENTIABLES. On se propose ici de les décrire dans un système de coordonnées et de voir comment cette description varie si l’on change de système. On appliquera ensuite ces calculs à l’étude des variétés pseudo-riemanniennes, en donnant des formules explicites pour la dérivée covariante.

1. Champs de vecteurs et formes de degré 1

Soit un système de coordonnées u ¹, ..., uⁿ au voisinage du point m ⁰ de E, de coordonnées u ¹⁰, ..., u ⁰ⁿ . Toute fonction numérique f définie sur E au voisinage de m ⁰ apparaît comme une fonction f ^u de n variables réelles: le nombre f ^u (u ¹, ..., u ⁿ ) est la valeur de f au point de coordonnées u ¹, ..., u ⁿ . On dit que f est de classe 暈 秊 si f ^u est une fonction de classe 暈 秊 d’un ouvert de Eⁿ dans R. Cette définition semble privilégier un système de coordonnées, mais il n’en est rien: en utilisant le fait que les changements de coordonnées sont de classe 暈 size=1^秊, on démontre que, pour tout autre système de coordonnées v ¹, ..., v ⁿ qui à f associe la fonction de n variables f ^v , la fonction f ^u est de classe 暈 size=1^秊 si et seulement si f ^v est de classe 暈 size=1^秊.

Un champ de vecteurs sur E (ou, plus précisément, avec les notations de l’article VARIÉTÉS DIFFÉRENTIABLES, un champ de vecteurs de classe 暈 size=1^秊; cf. aussi équations aux DÉRIVÉS PARTIELLES, chap. 1) est une correspondance X qui à toute fonction f de classe 暈 size=1^秊 associe une fonction X(f ) de classe 暈 size=1^秊 et vérifie les trois conditions suivantes:

a ) Si f et g coïncident au voisinage d’un point m , alors X(f ) et X(g ) coïncident au voisinage de m ;

b ) X(f +g ) = X(f ) +X(g ), où est une constante;

c ) X(fg ) = X(f )g + f X(g ).

On définit sur l’ensemble des champs de vecteurs une structure de module sur l’anneau des fonctions de classe 暈 size=1^秊 (cf. algèbre LINÉAIRE ET MULTILINÉAIRE, chap. 9) en posant:

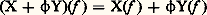pour toute fonction f . En associant à toute fonction f la fonction 煉f ^u / 煉u ⁱ , on définit un champ de vecteurs, que l’on notera 煉/ 煉u ⁱ . On montre que les n champs ainsi obtenus forment une base du module des champs; c’est-à-dire que, pour tout champ de vecteurs X, il existe une famille X¹, ..., Xⁿ de fonctions de classe 暈 size=1^秊, et une seule, telle que:

les Xⁱ sont appelées les coordonnées du champ X dans le système de coordonnées (u ¹, ..., u ⁿ ).

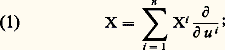Une forme de degré 1 est une correspondance 諸 qui à tout champ de vecteurs X associe une fonction 諸(X) de classe 暈 秊 et vérifie la condition suivante:

d ) Pour tout couple (X, Y) de champs de vecteurs et toute fonction 﨏 de classe 暈 size=1^秊, on a:

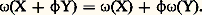Une forme de degré 1 est donc une application linéaire du module des champs dans l’anneau des fonctions de classe 暈 秊. En posant:

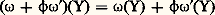pour tout champ de vecteurs Y, on munit l’ensemble des formes de degré 1 d’une structure de module sur l’anneau des fonctions de classe 暈 秊. La correspondance X 料 X(f ) est une forme de degré 1 pour toute fonction f de classe 暈 秊; on l’appelle la différentielle de f , et on la note df . Soit u ⁱ la fonction qui à tout point m associe sa i -ième coordonnée u ⁱ (m ) dans le système (u ¹, ..., u ⁿ ); les formes du ¹, ..., du ⁿ constituent une base du module des formes de degré 1, c’est-à-dire que, pour toute forme 諸, il existe une famille 諸¹, ..., 諸ⁿ de fonctions de classe 暈 size=1^秊, et une seule, telle que:

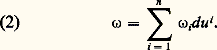Les fonctions 諸ⁱ sont appelées les coordonnées de la forme 諸 dans le système (u ¹, ..., u ⁿ ). On vérifie que:

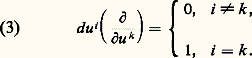Il en résulte que la valeur de la forme:

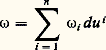sur le vecteur:

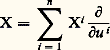est: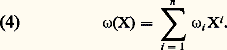

Changement de coordonnées

Soit maintenant un nouveau système de coordonnées (v ¹, ..., v ⁿ ). On a des fonctions de changement de coordonnées 﨏ⁱ et 祥^j telles que, pour tout m , on ait respectivement:

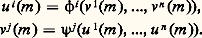Posons:

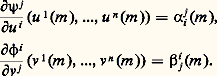Les matrices:

sont inversibles et inverses l’une de l’autre; on démontre les formules: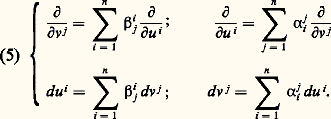

De ces formules on déduit que, si 諸 est une forme de degré 1 et X un champ de vecteurs dont les coordonnées dans les systèmes (u ¹, ..., u ⁿ ) et (v ¹, ..., v ⁿ ) sont respectivement les fonctions Xⁱ , X ^j , 諸ⁱ et 諸 ^j , on a:

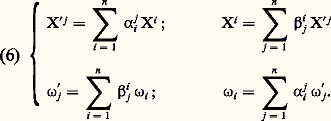2. Tenseurs

Tenseurs covariants

Un tenseur covariant à p variables 精 est une fonction, définie sur l’ensemble des systèmes de p champs de vecteurs et à valeurs dans l’anneau des fonctions de classe 暈 size=1^秊, qui est linéaire par rapport à chacune de ses variables, c’est-à-dire qui vérifie, pour tout k tel que 1 諒 k 諒 p , la condition L^k suivante: Pour tout système de vecteurs (X¹, ..., X^p ), avec X^k = Y + 﨏Z où 﨏 est une fonction de classe 暈 size=1^秊, on a:

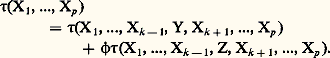Soit 諸¹, ..., 諸^p un système de p formes de degré 1. En associant à tout système de champs (X¹, ..., X^p ) le produit:

on définit un tenseur covariant à p variables que l’on note: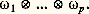

En particulier, si l’on s’est donné un système de coordonnées (u ¹, ..., u ⁿ ), alors, pour tout système i = (i ¹, ..., i ^p ) d’indices compris entre 1 et n , on a un tenseur:

on montre que les n ^p tenseurs ainsi définis forment une base du module des tenseurs covariants à p variables; c’est-à-dire que, pour tout tenseur covariant à p variables 精, il existe une famille ( 精^{i 1, ..., i p} ) de n ^p fonctions de classe 暈 size=1^秊, et une seule, telle que: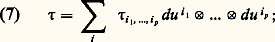

les fonctions 精^{i 1, ..., i p} sont les coordonnées du tenseur dans le système de coordonnées choisi.

Si l’on se donne un autre système de coordonnées (v ¹, ..., v ⁿ ), les formules (5) entraînent les formules (8) figurant dans le tableau.

On en déduit qu’entre les coordonnées 精^{i 1, ..., i p} du tenseur dans le système de coordonnées (u ¹, ..., u ⁿ ) et ses coordonnées 精 ^{j 1, ..., j p} dans le système de coordonnées (v ¹, ..., v ⁿ ) on a les relations (9) du tableau.

Tenseurs contravariants

De la même façon, on appelle tenseur contravariant à p variables une application, linéaire par rapport à chaque variable, de l’ensemble des systèmes de p formes de degré 1 dans l’anneau des fonctions de classe 暈 size=1^秊. Pour tout système d’indices i = (i ¹, ..., i ^p ), on définit le tenseur:

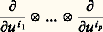par la formule:

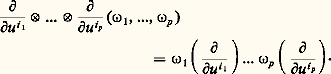Les n ^p tenseurs ainsi définis forment une base du module des tenseurs contravariants à p variables; donc, pour tout tenseur contravariant à p variables 精, on a une famille ( 精^{i 1, ..., i p} ) de fonctions de classe 暈 size=1^秊, et une seule, telle que la relation (10) du tableau soit satisfaite: les fonctions 精^{i 1, ..., i p} sont les coordonnées du tenseur dans le système de coordonnées (u ¹, ..., u ⁿ ).

Si maintenant les fonctions 精 ^{j 1, ..., j p} sont les coordonnées de 精 dans le système (v ¹, ..., v ⁿ ), on a les relations (10 ) du tableau.

Tenseurs de variance mixte

Soit (I, J) une partition de l’ensemble des entiers compris entre 1 et p . Un tenseur 精 de variance (I, J) est une fonction de p variables (A¹, ..., A^p ), linéaire par rapport à chacune d’elles, où A size=1^見 est une forme de degré 1 si 見 捻 I et un champ de vecteurs si 見 捻 J. L’ensemble I est l’ensemble des indices contravariants de 精 et J l’ensemble des indices covariants. Chaque système de coordonnées (u ¹, ..., u ⁿ ) définit une base (ayant n ^p éléments) du module des tenseurs de variance (I, J); donc 精 est déterminé, dans le système de coordonnées choisi, par n ^p fonctions coordonnées.

Par exemple, pour p = 3, un tenseur 精 de variance (face=F00191, 3, 2) associe à tout triplet ( 諸, X, 神), où X est un champ de vecteurs et 諸, 神 des formes de degré 1, une fonction 精( 諸, X, 神). Pour tout triplet (i ¹, i ², i ³) d’indices compris entre 1 et n , en associant à ( 諸, X, 神) la fonction produit:

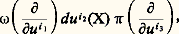on définit un tenseur de variance (face=F00191, 3, 2), que l’on note:

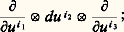les tenseurs de ce type forment une base, c’est-à-dire que, 精 étant donné, il existe une famille et une seule de n ³ fonctions de classe 暈 秊, que l’on notera ( 精^{i 1i 2i 3}), telle que:

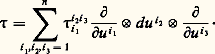Conventions de sommation

Dans tout ce qui précède, on a décrit un certain nombre de familles d’objets: bases du module des champs ou du module des formes de degré 1; coordonnées des champs, des formes, des tenseurs; dérivées partielles des changements de coordonnées. Les objets de chacune de ces familles sont alors repérés par un ou plusieurs indices compris entre 1 et n . On a placé certains de ces indices en haut , d’autres en bas . A priori, le choix de la place de ces indices paraît assez arbitraire; il n’en est rien. En effet, si on regarde toutes les formules de sommation qui ont été écrites, on constate que (à condition de considérer que, dans 煉/ 煉u ⁱ , l’indice i est en bas):

a ) Chaque fois qu’on a sommé par rapport à un indice, celui-ci apparaît deux fois dans la formule, une fois en haut et une fois en bas;

b ) Chaque fois qu’un indice apparaît deux fois, il est une fois en haut et une fois en bas, et on somme par rapport à lui.

Ces deux remarques permettent de retrouver assez facilement toutes les formules que l’on a écrites et, d’autre part, d’éliminer celles qui n’ont aucun sens intrinsèque. Par exemple, si on a deux champs X et Y de coordonnées Xⁱ et Yⁱ dans un certain système, on n’écrira jamais:

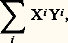car cette quantité dépend du système de coordonnées choisi; mais, si 諸 est une forme de degré 1, de coordonnées 諸ⁱ , la somme:

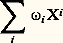est indépendante du système de coordonnées choisi.

On utilise cette convention pour l’écriture des tenseurs; on écrit les indices contravariants en haut et les indices covariants en bas. C’est ce que l’on a fait dans les exemples cités plus haut.

Comme les sommations que l’on doit faire sont indiquées par les indices, on prend l’habitude de supprimer les signes de sommation; c’est la convention d’Einstein . Ainsi, les formules (9) s’écrivent:

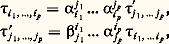La sommation par rapport aux indices j dans la première formule et par rapport aux indices i dans la seconde est indiquée par le fait que chacun de ces indices se trouve une fois en bas et une fois en haut.

La contraction

Ce principe de sommation, énoncé pour des indices de deux tenseurs différents, s’étend aux indices d’un même tenseur. Considérons, par exemple, un tenseur 精 à quatre indices, de coordonnées 精^{j ikl} dans un certain système de coordonnées; les quantités 精^{i ikl} , c’est-à-dire:

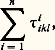sont les coordonnées d’un tenseur à deux variables, appelé le contracté de 精 par rapport aux deux premiers indices. De façon générale, chaque fois qu’un tenseur a un indice covariant et un indice contravariant, on peut les contracter et on obtient ainsi un tenseur qui a deux variables de moins que le tenseur que l’on contracte.

3. Variétés pseudo-riemanniennes

Nous écrirons désormais toutes les formules dans un système de coordonnées fixe (u ¹, ..., u ⁿ ), d’ailleurs arbitraire. Soit g un tenseur covariant à deux variables qui est symétrique, c’est-à-dire que g (X, Y) = g (Y, X) quels que soient X et Y. Les valeurs en un point m des coordonnées g ^ij de g forment une matrice carrée d’ordre n , et le déterminant de cette matrice dépend du système de coordonnées choisi; mais, s’il est nul dans un système, il l’est dans tous les autres. Si ce déterminant ne s’annule en aucun point m , on dit que g est une structure pseudo-riemannienne sur E (cf. VARIÉTÉS DIFFÉRENTIABLES, chap. 6). Dans ce qui suit, on fixe une fois pour toutes une structure pseudo-riemannienne g .

Soit X un champ de vecteurs; la correspondance qui à tout champ de vecteurs Y associe g (X, Y) est une forme de degré 1; on la note X size=1^寧. La correspondance qui à X associe X size=1^寧 est un isomorphisme du module des champs sur le module des formes; elle est donc biunivoque, et:

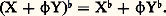Si on note Xⁱ les coordonnées de X, et Xⁱ size=1^寧 celles de X size=1^寧, on a, en utilisant les conventions de notations ci-dessus,

Cet isomorphisme 寧 se prolonge au cas des tenseurs: Si 精 est un tenseur dont l’indice 見 est contravariant, on définit un tenseur 精 size=1^寧( size=1^見) dont la variance diffère de celle de 精 par le fait que 見 y est covariant en posant, pour tout système de champs et de formes, (..., X, ...), où l’on n’a pas écrit les variables d’indice différent de 見: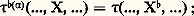

les coordonnées 精 size=1^寧( size=1^見)...i size=1^見... de 精 size=1^寧( 見) proviennent des coordonnées 精^...i size=1^見... de 精, grâce à la formule:

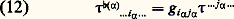Pour tout m , la matrice des coefficients g ^ij (m ) est inversible; soit g ^ij (m ) la matrice inverse. Les fonctions g ^ij sont de classe 暈 秊. Avec les conventions de notation que l’on a faites, le fait que la matrice (g ^ij (m )) soit l’inverse de la matrice (g ^ij (m )) se traduit par la formule:

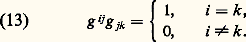De cette relation résulte que:

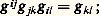autrement dit, le tenseur g est obtenu à partir du tenseur g de coordonnées g ^ij par application de 寧 (1) et 寧 (2).

On note 戀凉 les isomorphismes inverses des isomorphismes 寧 et on démontre que:

a ) Pour toute forme 諸 de degré 1, on a:

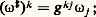b ) Pour tout tenseur 精 dont l’indice 見 est covariant, on a:

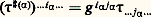On voit que l’on peut, grâce aux isomorphismes 寧 et 戀凉, modifier à volonté les variances des indices d’un tenseur. En particulier, on peut les rendre tous covariants ou tous contravariants. Les coordonnées du tenseur covariant associé à 精 sont appelées les coordonnées covariantes de 精 et celles du tenseur contravariant associé à 精 sont appelées les coordonnées contravariantes de 精. Les g ^ij sont donc les coordonnées contravariantes du tenseur métrique g et les g ^ij ses coordonnées covariantes. De même les Xⁱ sont les coordonnées contravariantes du champ X et les X^j = g ^ij Xⁱ ses coordonnées covariantes.

4. La dérivée covariante

Soit D une connexion linéaire sur E: à tout couple (X, Y) de champs de vecteurs elle associe un champ de vecteurs D^X Y tel que l’on ait les relations (cf. VARIÉTÉS DIFFÉRENTIABLES, chap. 7):

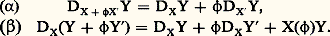Soit Xⁱ les coordonnées de X, soit Yⁱ celles de Y et 臨^{i jk} celles de:

dans le système de coordonnées (u ¹, ..., u ⁿ ). Des conditions ( 見) et ( 廓) on déduit:

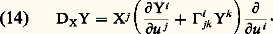Si D est la dérivée covariante (cf. VARIÉTÉS DIFFÉRENTIABLES, chap. 7), on montre que les 臨^{i jk} sont donnés par la formule:

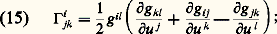on les appelle les symboles de Christoffel (cf. MÉCANIQUE ANALYTIQUE, chap. 3). On remarquera que, contrairement à ce qu’une analogie de notations pourrait laisser penser, les symboles de Christoffel ne se comportent pas comme les coordonnées d’un tenseur; c’est-à-dire que, si l’on exprime la dérivée covariante dans un autre système de coordonnées, on obtient d’autres fonctions 臨 ^{v uw} qui ne sont pas égales à:

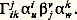Ces calculs permettent d’écrire de façon très simple le système différentiel des géodésiques: Soit 塚 une courbe paramétrée proportionnellement à sa longueur; c’est une géodésique si et seulement si:

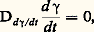c’est-à-dire si, en notant 塚ⁱ les fonctions coordonnées de 塚, on a:

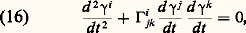quel que soit i .

Encyclopédie Universelle. 2012.